Econometrics often deals with complex models and datasets that may not align with the ideal assumptions of traditional statistical methods, such as large sample sizes, normality, or independent errors. When these assumptions are violated, standard techniques can yield unreliable results. Bootstrap methods address these challenges by offering a resampling-based approach to statistical inference.
By estimating parameters, correcting biases, and constructing confidence intervals without strict reliance on distributional assumptions, bootstrap methods provide flexibility and robustness. These techniques are particularly valuable in small samples and non-standard econometric models, enhancing the accuracy of analysis in challenging scenarios.
Introduction to Bootstrap Methods in Econometrics
Econometrics frequently involves drawing conclusions about populations based on limited sample data. Standard econometric techniques rely on strong assumptions, such as normality, large sample sizes, and independence of errors, to ensure reliable inference. However, real-world data often deviates from these assumptions. Small sample sizes, non-standard error distributions, and complex model structures can undermine the validity of traditional inference methods. This is where bootstrap methods step in as a transformative approach to statistical inference.
What Are Bootstrap Methods?
Bootstrap methods are data-driven techniques for estimating the sampling distribution of a statistic by resampling the observed data. Unlike traditional parametric methods, which depend on theoretical distributions (e.g., normal or t-distributions), bootstrap methods rely on the empirical data itself to construct estimates. By repeatedly drawing samples with replacement from the observed dataset, bootstrap methods allow researchers to approximate the variability of a statistic, construct confidence intervals, and test hypotheses without strict distributional assumptions.
For instance, in a simple scenario of estimating the mean income of a population from a sample, traditional methods might rely on the assumption that incomes follow a normal distribution. Bootstrap methods, on the other hand, avoid this assumption by directly resampling the observed incomes to estimate the variability of the mean.
The Historical Context
Bootstrap methods were introduced by Bradley Efron in the late 1970s, revolutionizing the field of statistical inference. Before the advent of bootstrap techniques, researchers faced significant challenges in cases where theoretical solutions were unavailable or unreliable due to small sample sizes or non-standard distributions. Efron’s innovation provided a computationally feasible solution that leveraged the growing availability of computing power to address these limitations.
Why Bootstrap Methods Matter in Econometrics
Flexibility Across Models
Bootstrap methods can be applied to a wide variety of econometric problems, from regression analysis to time series models, without requiring parametric assumptions.
Small-Sample Solutions
In cases where sample sizes are too small for asymptotic approximations to hold, bootstrap methods offer a practical alternative.
Robustness to Non-Normality
Many economic variables, such as income, asset returns, or firm performance, exhibit skewed or heavy-tailed distributions. Bootstrap methods handle such complexities effectively.
Improved Confidence Intervals and Hypothesis Testing
Traditional methods rely on theoretical approximations to construct confidence intervals and test statistics. Bootstrap methods derive these intervals and statistics empirically, leading to more accurate inference.
The Bootstrap Algorithm
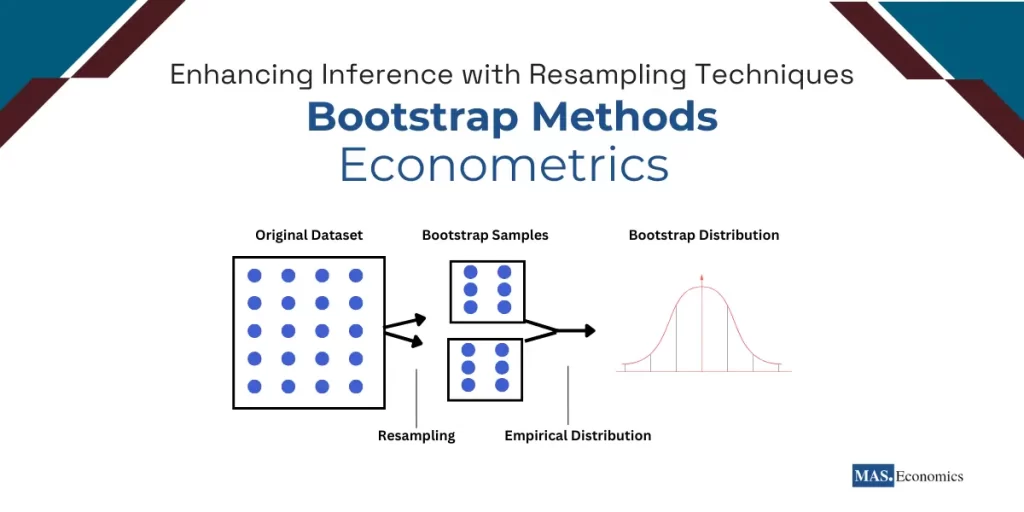
The bootstrap algorithm forms the backbone of bootstrap methods. It provides a systematic approach to generating a sampling distribution for a statistic by resampling from the observed data. This empirical method eliminates the reliance on theoretical assumptions, making it particularly useful in situations where the underlying distribution of the data is unknown or complex.
Steps in the Bootstrap Algorithm
-
Start with the Original Dataset:
Begin with a dataset of size \( n \), denoted as \( X = \{x_1, x_2, \ldots, x_n\} \). This dataset is assumed to be a representative sample from the population.
-
Resample with Replacement:
Create a bootstrap sample \( X^* \) by randomly drawing \( n \) observations from \( X \), with replacement. Each bootstrap sample may include duplicate observations and exclude others, reflecting the variability inherent in random sampling.
-
Compute the Statistic of Interest:
Calculate the statistic (e.g., mean, variance, regression coefficient) for the bootstrap sample \( X^* \).
-
Repeat the Process:
Repeat steps 2 and 3 \( B \) times (typically \( B = 1,000 \) or more) to generate a distribution of the statistic across bootstrap samples.
-
Analyze the Bootstrap Distribution:
Use the bootstrap distribution to draw inferences, such as:
- Estimating standard errors by computing the standard deviation of the bootstrap statistics.
- Constructing confidence intervals using the percentiles of the bootstrap distribution.
- Testing hypotheses by comparing the observed statistic to the bootstrap distribution.
Example: Estimating the Mean Income
Suppose we have a dataset of 10 individuals’ incomes (\$40k, \$50k, \$55k, \$60k, \$65k, \$70k, \$75k, \$80k, \$85k, \$90k). To estimate the sampling distribution of the mean income using the bootstrap algorithm:
- Resample the 10 observations with replacement to create a bootstrap sample (e.g., \$50k, \$55k, \$55k, \$70k, \$90k, \$70k, \$65k, \$40k, \$85k, \$55k).
- Compute the mean income for this bootstrap sample (\$63k).
- Repeat this process \( B = 1,000 \) times to generate 1,000 mean income estimates.
- Use the bootstrap distribution of the mean to compute the standard error, confidence intervals, or p-values for hypothesis testing.
Advantages of the Bootstrap Algorithm
Simplicity
The bootstrap algorithm is conceptually straightforward, making it accessible even for researchers without advanced statistical backgrounds.
Computational Feasibility
With modern computing power, resampling thousands of times is practical, even for large datasets or complex models.
Distribution-Free Inference
The bootstrap algorithm does not require knowledge of the underlying data distribution, providing robust inference in non-standard scenarios.
Applicability to Complex Models
The algorithm extends seamlessly to regression models, time series analysis, and other advanced econometric frameworks, offering reliable estimates where analytical solutions may not exist.
Challenges of the Bootstrap Algorithm
Dependence on Sample Quality
The validity of bootstrap methods hinges on the assumption that the observed sample accurately represents the population. If the sample is biased or unrepresentative, bootstrap estimates will inherit these flaws.
Computational Intensity
Resampling and recalculating statistics thousands of times can be computationally demanding, particularly for large datasets or complex models.
Finite Sample Limitations
In very small samples, bootstrap methods may not adequately capture the variability of the population, leading to underestimation of uncertainty.
Key Applications of Bootstrap Methods in Econometrics
Bootstrap methods offer robust solutions to econometric challenges, especially in cases where traditional methods fall short due to small sample sizes, complex models, or non-standard assumptions. Below are key areas where bootstrap methods are transformative:
Bias Correction for Estimators
In econometrics, estimators often exhibit bias in small samples or non-linear models. Bootstrap methods address this by resampling the data to compute the average bias and adjust the original estimate accordingly.
Example: In nonlinear regression models, small-sample biases can distort parameter estimates. By recalculating these estimates across bootstrap samples, researchers can accurately correct for the bias, ensuring reliability even in limited data settings.
Constructing Reliable Confidence Intervals
Bootstrap methods are invaluable for constructing confidence intervals in scenarios where traditional parametric methods fail. By empirically deriving confidence intervals from the bootstrap distribution, they account for skewness, heavy tails, and other deviations from normality.
Example:
In financial econometrics, bootstrap confidence intervals are used to estimate parameters like portfolio risk or volatility. This approach provides accurate interval estimates for non-normal data, such as asset returns, which often exhibit heavy tails and outliers.
Hypothesis Testing
Traditional hypothesis testing relies on theoretical distributions of test statistics, which may not hold under non-standard conditions. Bootstrap methods generate empirical p-values by resampling the data and constructing a distribution of the test statistic under the null hypothesis.
Example:
In financial markets, when testing whether two assets yield the same risk-adjusted return, bootstrap methods account for the skewness and kurtosis of return distributions, providing robust p-values for more reliable inference.
Improved Standard Error Estimation
Complex econometric models often involve parameters with standard errors that are difficult to derive analytically. Bootstrap methods estimate these standard errors empirically, leveraging the variability of resampled datasets to compute robust estimates.
Example:
In dynamic panel data models estimated via generalized method of moments (GMM), bootstrap methods produce robust standard errors that account for heteroskedasticity and serial correlation, improving the reliability of policy analysis.
Applications in Time Series Econometrics
Time series data often exhibit autocorrelation, volatility clustering, and non-stationarity, violating the assumptions of parametric methods. Bootstrap techniques, such as block bootstrapping, account for these dependencies, preserving the temporal structure of the data while providing reliable inference.
Example:
In energy economics, block bootstrap methods help forecast renewable energy prices by capturing autocorrelations in historical data, enabling policymakers to design more effective pricing strategies for carbon credits and energy subsidies.cal implications for pricing renewable energy credits or forecasting oil prices under uncertain market conditions.
Conclusion
Bootstrap methods provide robust solutions in econometrics by leveraging data resampling to overcome the limitations of traditional statistical techniques. These methods are especially effective in small-sample settings, complex models, and scenarios where standard assumptions, such as normality or independence, do not hold. Applications like bias correction, hypothesis testing, and robust standard error estimation make bootstrap methods invaluable for enhancing the reliability of econometric analysis.
Advancements in computational capabilities have expanded the applicability of bootstrap methods, enabling their use in addressing more complex econometric challenges and improving the precision of statistical results.
FAQs:
What are bootstrap methods in econometrics?
Bootstrap methods are resampling techniques that estimate the sampling distribution of a statistic by repeatedly drawing samples with replacement from the observed data. They enable statistical inference without relying on strict distributional assumptions, making them robust for small sample sizes and non-standard models.
Why are bootstrap methods preferred in small-sample econometric models?
Bootstrap methods are preferred in small-sample contexts because they do not depend on large-sample approximations. By resampling the available data, they provide accurate estimates of variability, correct biases, and construct confidence intervals even when traditional methods fail.
How do bootstrap methods improve confidence intervals in econometrics?
Bootstrap methods create confidence intervals by empirically generating a distribution of the statistic from resampled datasets. This approach accounts for skewness, heavy tails, and other deviations from normality, making the intervals more reliable and accurate in non-standard scenarios.
What challenges do bootstrap methods address in hypothesis testing?
Bootstrap methods handle challenges in hypothesis testing by empirically constructing the distribution of the test statistic under the null hypothesis. This is especially useful when theoretical distributions are unreliable due to non-normality, heteroskedasticity, or other complexities in the data.
Where are bootstrap methods commonly applied in econometrics?
Bootstrap methods are widely applied in dynamic panel data analysis, time series econometrics, and financial modeling. They are used to estimate robust standard errors, evaluate bias in parameter estimates, and analyze complex models with dependencies or non-standard distributions.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics