Econometric models often rely on assumptions about the functional form of relationships between variables. Traditional parametric methods, like Ordinary Least Squares (OLS) and Maximum Likelihood Estimation (MLE), require specific assumptions, such as linearity, that may not align with the complexities of real-world data. When these assumptions fail, the resulting models can yield biased or unreliable results.
Nonparametric and semiparametric methods address this limitation by offering greater flexibility in analyzing data. These approaches do not impose rigid assumptions about the functional form, allowing for the identification of complex, nonlinear, or unknown patterns in relationships. By relying more on the data itself, they provide a robust alternative for modeling intricate economic phenomena.
Introduction to Nonparametric and Semiparametric Methods
Econometric analysis often involves assumptions about the functional form of relationships between variables. Traditional parametric methods, such as linear regression and logit models, rely on predefined mathematical relationships, like linear or quadratic forms. These models are computationally efficient and easy to interpret but are heavily dependent on the validity of their underlying assumptions. For instance, a linear regression assumes that the relationship between dependent and independent variables is linear. However, if the true relationship is nonlinear or more complex, the model will produce biased or misleading results.
What Are Nonparametric and Semiparametric Methods?
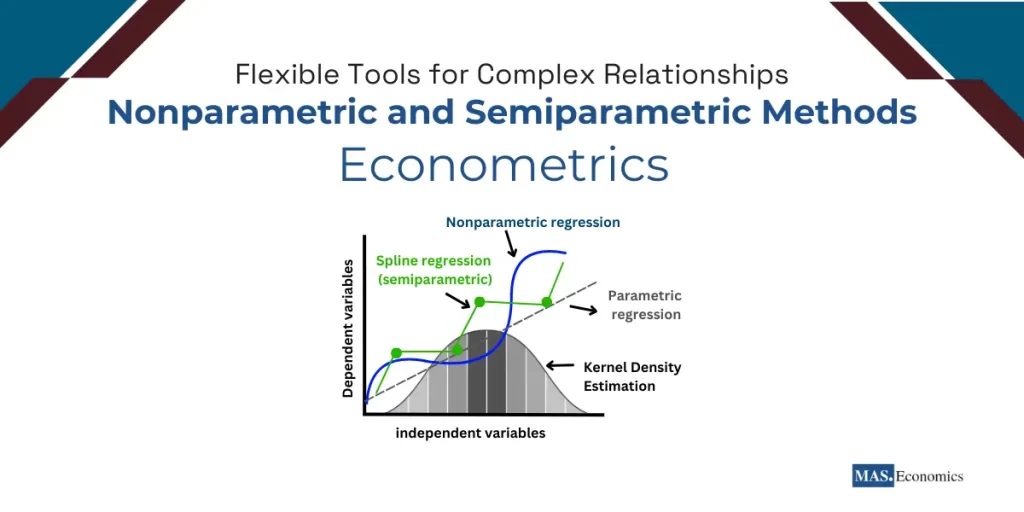
Nonparametric methods do not impose strict assumptions about the relationship between variables. They rely on data-driven techniques that let the data dictate the structure of the model, making them particularly useful for capturing nonlinearities and unexpected patterns. Examples of nonparametric methods include kernel density estimation, local polynomial regression, and k-nearest neighbors.
Semiparametric methods combine the interpretability of parametric models with the flexibility of nonparametric techniques. They specify part of the model parametrically while leaving other parts flexible. For instance, spline regression is a semiparametric method that models relationships using piecewise polynomial functions.
Why These Methods Matter in Econometrics
These methods are particularly valuable in contexts where rigid assumptions may obscure meaningful insights. Economic data often exhibit nonlinearities, interactions, and heterogeneity that parametric models fail to capture. By adapting to the data’s structure, nonparametric and semiparametric methods mitigate the risk of model misspecification, making them essential tools for exploratory analysis and hypothesis generation. Their applications range from income distribution modeling to demand forecasting and consumer behavior studies, where traditional parametric approaches may fall short.
Advantages Over Parametric Approaches
Parametric methods remain a cornerstone of econometrics due to their simplicity, interpretability, and computational efficiency. However, they come with limitations, particularly in contexts where the true functional form of the relationship between variables is unknown or highly nonlinear. Nonparametric and semiparametric methods offer several advantages in such situations.
Handling Nonlinear Relationships
Nonparametric methods excel at capturing complex, nonlinear relationships that parametric models struggle to handle. For instance:
- In demand forecasting, the relationship between price and demand may follow a U-shape, where demand increases with price up to a point before declining. Nonparametric regression can model this pattern directly from the data without assuming a predefined form.
Flexibility and Adaptability
Nonparametric methods are inherently flexible, adapting to the data’s structure rather than imposing an external form. This is particularly useful in exploratory analyses where the goal is to uncover patterns or generate hypotheses.
Reducing Misspecification Bias
Parametric models are prone to misspecification bias when their assumptions (e.g., linearity, normality) do not align with the data. Nonparametric methods avoid this risk by allowing the data to guide the model structure.
Capturing Heterogeneity
Economic data often exhibit heterogeneity across individuals, firms, or markets. Semiparametric methods, such as partially linear models, allow for flexibility in some parts of the model while retaining structure in others. For example:
- A semiparametric model might use a flexible nonparametric component to account for regional differences in consumer behavior while maintaining a linear relationship between income and spending at the individual level.
Robustness in High-Dimensional Settings
Semiparametric models, such as additive models, handle high-dimensional data more efficiently than fully parametric or nonparametric approaches, balancing flexibility and interpretability.
Key Techniques
Kernel Density Estimation (KDE)
Kernel density estimation (KDE) is a fundamental nonparametric method used to estimate the probability density function (PDF) of a random variable. Unlike histograms, which divide data into discrete bins, KDE provides a smooth and continuous estimate of the underlying distribution, making it ideal for identifying patterns like multimodal distributions.
How It Works
KDE assigns a “kernel” function, such as a Gaussian curve, to each data point and combines these kernels to estimate the density. The smoothness of the estimate is controlled by the bandwidth parameter, which determines the width of the kernel. A smaller bandwidth results in a more sensitive estimate, capturing finer details, while a larger bandwidth produces a smoother, less sensitive curve.
The formula for KDE is:
-
Kernel Function: Each data point contributes a kernel function (e.g., a Gaussian curve) centered at its value.
-
Bandwidth (\( h \)): Controls the smoothness of the estimate. A smaller \( h \) results in a more sensitive estimate, while a larger \( h \) produces a smoother curve.
The KDE formula is:
Where:
- \( \hat{f}(x) \): Estimated density at \( x \).
- \( K(\cdot) \): Kernel function (e.g., Gaussian, Epanechnikov).
- \( h \): Bandwidth.
- \( X_i \): Observed data points.
Applications
KDE is widely used in econometrics for tasks like income distribution modeling and consumer behavior analysis:
- In income distribution analysis, KDE can reveal patterns of inequality by estimating the density of household incomes.
- In consumer spending analysis, KDE can identify variations in spending across demographic groups or regions.
Challenges
While KDE is flexible and powerful, it requires careful selection of the bandwidth parameter, as it significantly impacts the results. Computational intensity can also become an issue for large datasets.
Spline Regression
Spline regression is a semiparametric technique that models relationships using piecewise polynomial functions. It is particularly effective in capturing nonlinear relationships, making it a valuable tool for analyzing economic data.
How It Works
Spline regression divides the range of the predictor variable into intervals and fits a polynomial function within each interval. These polynomials are joined smoothly at predetermined points called knots to ensure continuity and smoothness.
A cubic spline model can be written as:
Where:
- \( \kappa_k \): Knot location.
- \( (X – \kappa_k)^3_+ \): The cubic spline basis function.
Applications
Spline regression is commonly used in scenarios where relationships vary across different ranges of the predictor variable:
- In demand forecasting, splines can model how demand responds to price changes at various price levels, capturing shifts in consumer behavior.
- In economic growth analysis, spline regression can capture growth trends that change during recessions or periods of rapid development.
Strengths and Challenges
Spline regression strikes a balance between flexibility and interpretability. By fitting polynomials within intervals, it avoids overfitting while allowing the model to adapt to local variations. However, the placement and number of knots require careful consideration to ensure the model captures meaningful patterns without becoming overly complex.
Applications in Econometrics
Modeling Income Distribution
Nonparametric methods like KDE provide unparalleled flexibility in analyzing income distributions, allowing researchers to estimate multimodal distributions and detect patterns of inequality. For instance:
- KDE has been used to compare income inequality across regions, highlighting disparities between urban and rural areas.
- By avoiding predefined assumptions, nonparametric methods can uncover unexpected clustering in middle-income brackets or tails of the distribution.
Analyzing Consumer Behavior
Semiparametric models are particularly effective in understanding complex consumer behavior patterns without imposing linearity. For example:
- Spline Regression: Models how advertising expenditures influence sales at different levels, capturing diminishing returns or saturation effects.
- Partially Linear Models: Analyze how income levels impact consumer preferences for luxury goods, accounting for nonlinear relationships while controlling for demographic factors.
Forecasting Demand in Dynamic Markets
In markets where price-demand relationships are nonlinear or influenced by external factors, nonparametric regression excels:
- Forecast how consumer demand for electric vehicles changes as government subsidies vary across regions.
- Use spline regression to incorporate seasonality into demand forecasting for agricultural products.
Applications in Financial Markets
Nonparametric methods are increasingly used to analyze complex financial data. For example:
- Volatility Modeling: Kernel regression can estimate volatility clustering in stock prices, revealing how past volatility impacts future returns.
- Risk Assessment: Nonparametric density estimation identifies the distribution of portfolio returns, providing insights into tail risks.
Conclusion
Nonparametric and semiparametric methods provide versatile tools for analyzing economic data without the constraints of predefined functional forms. Techniques like kernel density estimation and spline regression enable researchers to uncover complex, nonlinear, or previously hidden patterns in relationships.
These methods are widely used in applications such as modeling income distribution, analyzing consumer behavior, and forecasting demand, providing effective alternatives to traditional parametric models in addressing specific econometric challenges.
FAQs:
What are nonparametric and semiparametric methods in econometrics?
Nonparametric and semiparametric methods are flexible econometric techniques that do not rely on strict assumptions about the functional form of relationships between variables. Nonparametric methods let the data dictate the structure of the model, while semiparametric methods combine parametric and nonparametric components to balance interpretability and flexibility.
Why are nonparametric and semiparametric methods important in econometrics?
These methods are important because they allow researchers to model complex, nonlinear relationships and avoid biases caused by incorrect assumptions in parametric models. They are particularly useful when the true relationship between variables is unknown or highly nonlinear, making them valuable for exploratory analysis and hypothesis testing.
How does kernel density estimation (KDE) work in nonparametric analysis?
Kernel density estimation (KDE) is a nonparametric method for estimating the probability density function of a random variable. It uses kernel functions, such as Gaussian curves, centered on each data point and combines them to create a smooth density estimate. The bandwidth parameter controls the smoothness, with smaller bandwidths capturing finer details and larger ones producing smoother estimates.
What is spline regression, and how is it used in semiparametric modeling?
Spline regression is a semiparametric technique that models relationships using piecewise polynomial functions joined smoothly at points called knots. It is commonly used to capture nonlinear relationships in data, such as changes in demand at different price levels or shifts in economic growth trends during recessions or periods of rapid development.
What are the advantages of nonparametric methods over parametric approaches?
Nonparametric methods offer flexibility in capturing nonlinear and complex relationships, reduce the risk of misspecification bias, and adapt to the data’s structure. Unlike parametric models, they do not require predefined assumptions about the relationship between variables, making them more robust in exploratory and high-dimensional analyses.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics