Econometrics is often used to analyze relationships between variables, identify patterns, and test hypotheses. However, many critical aspects of real-world phenomena—like intelligence, consumer satisfaction, or economic stability—are latent constructs that cannot be directly measured. These unobservable factors significantly influence observable variables, presenting a challenge for traditional econometric models.
Structural Equation Models (SEM) address this limitation by offering a statistical framework to estimate relationships between both latent and observed variables simultaneously. By integrating regression analysis, factor analysis, and path analysis, SEM connects theoretical constructs with empirical data, enabling the study of complex systems.
Key Components of SEM
Structural Equation Models (SEM) center on several core components that make them uniquely powerful for analyzing relationships between variables. These components—latent variables, path diagrams, and causal inference—allow SEM to model hidden constructs, visualize complex relationships, and test cause-and-effect hypotheses within a unified framework.
Latent Variables
Latent variables are central to SEM’s ability to capture abstract concepts that influence observable behaviors or outcomes. Unlike directly measurable variables, latent variables represent constructs such as intelligence, consumer satisfaction, or economic stability that can only be inferred through their observable indicators.
How Latent Variables Work
Latent variables are integrated into SEM models through measurement models, which link observed indicators to the underlying construct. For instance:
- Consumer Confidence might be inferred from survey responses on spending intentions, savings behavior, and economic optimism.
- Health Outcomes can be measured using recovery rates, patient satisfaction scores, and access to preventive care.
In this way, SEM uncovers hidden drivers of behavior or outcomes and explicitly accounts for measurement error. Factor loadings quantify how well each observable indicator reflects the latent construct, ensuring robust estimates.
Importance in Econometrics
Latent variables enable researchers to address questions that involve unobservable factors shaping economic and social systems. For example:
- In labor economics, job satisfaction (latent) helps explain variations in productivity and employee turnover.
- In macroeconomics, economic resilience (latent) sheds light on how countries recover from recessions, linking fiscal health and institutional strength to observed GDP growth.
By incorporating latent variables, SEM allows economists to merge theoretical constructs with real-world data, bridging the gap between abstract concepts and measurable outcomes.
Path Diagrams
What Are Path Diagrams?
Path diagrams are visual representations of SEM models that illustrate relationships between variables. They simplify potentially complex models by showing causal pathways, correlations, and dependencies in an accessible format.
Elements of Path Diagrams
- Observed Variables (rectangles)
- Latent Variables (ovals)
- Arrows:
- Single-Headed Arrows: Indicate causal relationships (e.g., education → income).
- Double-Headed Arrows: Represent correlations without implying causality (e.g., income ↔ savings).
The following illustration visually summarizes the key components of path diagrams:
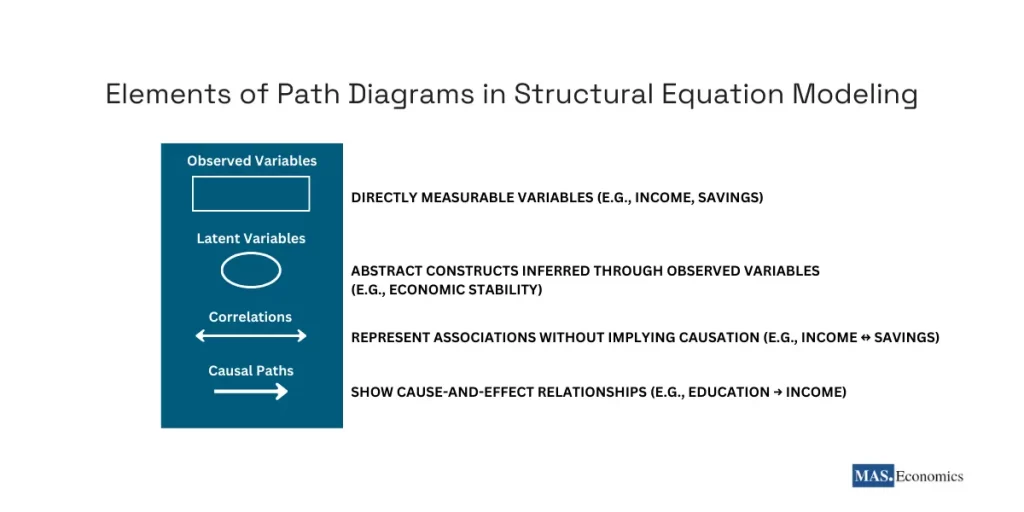
This illustration highlights the core elements of path diagrams, showing how SEM integrates observed variables, latent variables, correlations, and causal paths into a cohesive framework.
How Path Diagrams Enhance SEM Models
Path diagrams serve as blueprints for both the structural model (showing how variables influence each other) and the measurement model (showing how latent variables are inferred). By visually highlighting mediating and moderating effects, they help researchers and stakeholders alike understand key pathways—for instance, whether education influences economic well-being directly or indirectly through higher income.
Applications of Path Diagrams
Path diagrams are widely used to communicate SEM insights in various fields. For example:
- Finance: A path diagram might depict how risk perception moderates the link between economic uncertainty and investment decisions.
- Healthcare: It could show how access to care mediates the relationship between socioeconomic status and health outcomes.
Causal Inference
How SEM Facilitates Causal Inference
SEM goes beyond traditional correlations to test hypotheses about cause-and-effect relationships. Its flexibility accommodates multiple pathways, mediating variables, and feedback loops, making it a robust framework for exploring dynamic systems.
- Direct Effects: Immediate impact of one variable on another (e.g., interest rates → investment).
- Indirect Effects: One variable’s influence on another through a mediator (e.g., education → skills → income).
- Feedback Loops: Reciprocal relationships, such as how inflation expectations influence actual inflation over time.
Advantages of SEM for Causal Analysis
- Mediating Effects: Identifies which variables function as intermediaries (e.g., fiscal policy → infrastructure → GDP growth).
- Simultaneous Testing: Allows researchers to test multiple hypotheses in one cohesive model.
- Complex Pathways: Models direct and indirect routes simultaneously, clarifying how a single policy can affect multiple outcomes.
Applications in Econometrics
SEM excels in analyzing causal mechanisms in economic systems. Examples include:
- Policy Evaluation: Determining how monetary policy influences employment through investment and consumer spending.
- Market Behavior: Uncovering how advertising affects consumer loyalty through product satisfaction.
Challenges in Causal Inference
Like all modeling approaches, SEM depends on solid theoretical assumptions and accurate model specifications. Mis-specification can produce biased estimates, highlighting the importance of rigorous testing and model refinement.
Bridging Theory and Data
A vital advantage of Structural Equation Models (SEM) is their ability to link theoretical constructs with empirical data. Researchers often begin with concepts that cannot be directly measured or with hypotheses involving intricate interdependencies. SEM provides a structured methodology to bring these abstract ideas into alignment with observable evidence.
Integrating Latent Constructs
Many economic theories hinge on intangible concepts like economic resilience or consumer confidence. SEM incorporates these constructs into models, validating their effect on real-world outcomes:
- Economic Resilience (latent) can be inferred from GDP growth volatility, unemployment rates, and fiscal deficits.
- Consumer Confidence (latent) can be represented through survey data on spending habits and savings rates.
By capturing latent constructs explicitly, SEM helps researchers determine which parts of the theory hold up against empirical evidence.
Capturing Complex Relationships
Economic systems frequently exhibit simultaneous direct and indirect effects, along with possible feedback loops. SEM allows for all these pathways to be evaluated at once. A researcher exploring how government spending drives GDP growth might test both a direct route (government spending → GDP) and indirect routes (government spending → infrastructure → private investment → GDP).
Testing Hypotheses
SEM’s framework clarifies how well data aligns with hypothesized causal links:
- If a theory posits that infrastructure investment improves productivity, SEM can identify if this relationship is contingent on complementary factors like an educated workforce or regulatory environment.
- Unexpected paths or inconsistencies may prompt refinements to the original theory, fostering a cycle of continuous improvement between hypothesis and observation.
Case Study: Modeling Government Spending and GDP
A study on government spending might propose:
- Direct Path: Government spending → GDP growth.
- Indirect Path: Government spending → infrastructure → private investment → GDP growth.
SEM could reveal that infrastructure development explains 60% of the observed GDP boost, while private-sector investment contributes an additional 30%. These findings guide policymakers to target spending where it yields optimal long-term returns.
Practical Applications of SEM
Structural Equation Models (SEM) have diverse applications, offering insights into systems and uncovering hidden dynamics in various fields.
Education
SEM is used to analyze factors influencing student performance by integrating latent variables like motivation, engagement, or school climate. For example:
- Student Motivation may be inferred from attendance rates and homework completion.
- Teacher Quality and School Resources might be specified as direct predictors of student engagement.
This approach helps pinpoint interventions most likely to improve academic outcomes—such as teacher training programs or enhanced learning materials.
Healthcare
Healthcare systems involve interconnected elements: socioeconomic status, health behaviors, access to care, and more. SEM provides a unified model to examine these links:
- Latent Variable: “Health Outcomes” might include recovery rates and patient satisfaction.
- Causal Pathways: Socioeconomic variables (income, education) may influence health through access to preventive services.
By showing which pathways matter most, SEM helps policymakers prioritize equitable healthcare accessibility.
Economics
Economics is a leading domain for SEM due to the complexity of macroeconomic and market phenomena:
Modeling Monetary Policy Effects
Interest rate changes affect both consumption and investment, which in turn influence inflation and employment:
- Direct Effect: Lower rates → more investment and consumption.
- Indirect Effect: Cheaper borrowing → improved household liquidity → further economic impacts.
SEM can quantify each effect’s contribution, guiding central banks in meeting inflation or employment targets.
Investigating Consumer Confidence
Consumer confidence is a latent construct that drives aggregate demand. SEM reveals how shifts in optimism translate into spending and savings patterns:
- A 10% dip in consumer confidence might result in a 5% drop in discretionary spending, producing ripple effects on GDP and unemployment.
Linking Fiscal Policies to Unemployment
SEM can dissect how public spending, taxation, and subsidies jointly influence job creation:
- Direct Effect: Jobs created by infrastructure projects.
- Indirect Effect: Increased disposable income boosting private sector demand.
A study might find that a $1 billion infrastructure investment reduces unemployment by 0.5 percentage points overall, with 60% due to direct job creation and 40% due to private-sector spillovers.
Conclusion
Structural Equation Models (SEM) offer a robust framework for analyzing relationships among observed and latent variables, seamlessly connecting theoretical constructs with empirical data. By utilizing path diagrams and carefully modeling latent factors, SEM provides insights into complex systems that traditional econometric methods often miss.
SEM’s applications span diverse fields, including education, healthcare, and economics, where it effectively uncovers hidden constructs and their influence on measurable outcomes. It remains a valuable approach for addressing the complexities of data-driven research and understanding latent-variable relationships.
FAQs:
What are Structural Equation Models (SEM)?
Structural Equation Models (SEM) are statistical frameworks that estimate relationships between both latent (unobservable) and observed variables. They combine regression analysis, factor analysis, and path analysis to study complex systems, allowing researchers to connect theoretical constructs with empirical data.
Why are latent variables important in SEM?
Latent variables represent unobservable constructs like intelligence, consumer confidence, or economic stability, which influence observable outcomes. SEM uses measurement models to link these latent variables to observed indicators, accounting for measurement errors and providing insights into the hidden drivers of behavior or outcomes.
How do path diagrams enhance Structural Equation Models?
Path diagrams visually represent the relationships between variables in SEM. They highlight causal pathways, correlations, and dependencies, making complex models easier to understand. These diagrams help researchers communicate how variables influence each other, including direct, indirect, and mediating effects.
What is the role of SEM in causal inference?
SEM facilitates causal inference by modeling direct, indirect, and feedback effects between variables. For example, it can analyze how fiscal policy influences GDP growth directly and indirectly through infrastructure and private investment, providing a comprehensive understanding of cause-and-effect relationships.
How does SEM bridge theory and empirical data?
SEM connects theoretical constructs, like economic resilience or consumer confidence, with measurable outcomes by incorporating latent variables. It evaluates how well data aligns with hypothesized causal links, identifying areas where theory holds true and prompting refinements when inconsistencies arise.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics




