Choosing the best econometric model is a crucial step in the data analysis process. Building on what we’ve learned in previous posts—like the fundamentals of simple and multiple regression models, how to manage heteroscedasticity, address autocorrelation, and tackle multicollinearity—this post will focus on selecting a model that balances complexity and accuracy. The goal is to find a model that not only fits the data well but also serves as a reliable tool for forecasting and interpretation. This ensures that your analysis remains robust, whether you’re forecasting economic indicators or assessing policy impacts.
In this post, we will explore:
- Why model selection is important
- Criteria for choosing the best regression model, including Adjusted R², AIC, BIC, and others
- Model selection techniques like stepwise regression and all-possible regressions
- Practical examples using economic data
- Common challenges in model selection and how to address them
Why Model Selection Matters
Model selection is an essential step in econometric analysis. The goal is to avoid common pitfalls such as:
Overfitting
A model that is too complex may fit the data perfectly but fails to generalize to new data. This is like adding too many variables to a multiple regression model, leading to a high R² but poor predictive performance.
Underfitting
A model that is too simple might miss important relationships between variables, leading to inaccurate predictions. For instance, relying solely on a simple regression model when a multiple regression model is needed can ignore crucial factors affecting your dependent variable.
Including Irrelevant Variables
Adding variables that do not significantly contribute to the model’s explanation of the dependent variable can inflate standard errors, reduce the efficiency of estimators, and complicate the interpretation of results.
Choosing the right model ensures that the relationships identified in the data are both statistically valid and economically meaningful, helping to bridge the gap between theory and empirical evidence—one of the core functions of econometrics.
Common Criteria for Model Selection
Selecting the best regression model often involves balancing goodness of fit with model simplicity. Several statistical criteria help us strike this balance:
Adjusted R²
In our earlier posts, we discussed R² as a measure of how well the independent variables explain the variation in the dependent variable. Adjusted R² takes this a step further by accounting for the number of predictors in the model, providing a more accurate measure when comparing models with different numbers of variables.
- \( R^2 \) is the coefficient of determination.
- \( n \) is the number of observations.
- \( p \) is the number of predictors.
Adjusted R² is particularly valuable when working with multiple regression models. It helps to ensure that only variables that improve the model’s fit are included, avoiding unnecessary complexity.
Akaike Information Criterion (AIC)
The Akaike Information Criterion (AIC) is a widely used measure for selecting models based on the principle of entropy. AIC rewards models that fit the data well while penalizing those that include too many parameters:
- \( k \) is the number of parameters in the model.
- \( L \) is the likelihood function.
A lower AIC value indicates a better balance between fit and simplicity. This is particularly useful when deciding between models that explain economic phenomena, such as predicting GDP growth using several macroeconomic indicators like interest rates and inflation.
Bayesian Information Criterion (BIC)
The Bayesian Information Criterion (BIC) is similar to AIC but imposes a stronger penalty for adding additional parameters. It is particularly useful when you want to ensure parsimony in your model:
- \( n \) is the number of observations.
- \( k \) is the number of parameters.
BIC is often preferred in financial econometrics or macroeconomic forecasting, where simpler models tend to generalize better. It is a more conservative measure than AIC, making it suitable when avoiding overfitting is crucial.
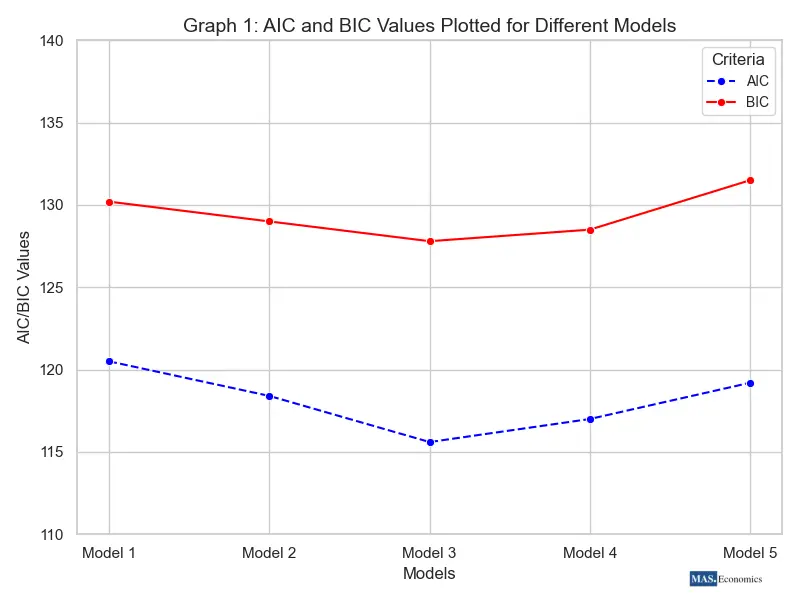
Graph 1 visualizes the AIC and BIC values for various models. Both values generally decrease as the model improves, with the lowest points indicating the best balance between fit and complexity. AIC is less penalizing for additional parameters compared to BIC, which tends to prefer simpler models. This graph aids in selecting the optimal model based on both criteria.
Mallows’ Cp
Mallows’ Cp is a criterion that balances the trade-off between bias and variance. It is particularly useful when comparing models with different numbers of variables:
- \( RSS \) is the residual sum of squares.
- \( \hat{\sigma}^2 \) is the estimated variance of the error term.
- \( p \) is the number of predictors.
A good model will have a Cp value close to the number of predictors, indicating that it is neither overfitting nor underfitting the data.
The following table shows a comparison of Adjusted R², AIC, BIC, and Mallows’ Cp for regression model subsets
| Model Subset | Adjusted R² | AIC | BIC | Mallows’ Cp |
|---|---|---|---|---|
| Model 1 | 0.85 | 120.5 | 130.2 | 2.5 |
| Model 2 | 0.88 | 118.4 | 129.0 | 3.1 |
| Model 3 | 0.90 | 115.6 | 127.8 | 4.0 |
| Model 4 | 0.89 | 117.0 | 128.5 | 4.2 |
| Model 5 | 0.87 | 119.2 | 131.5 | 5.0 |
 | ||||
Table showing Model 3 has the lowest AIC and BIC, indicating the best balance between fit and complexity, with adjusted R² values ranging from 0.85 to 0.90.
Econometric Model Selection Procedures
Building on the foundational knowledge from simple and multiple regression models, we now look at some systematic approaches for selecting the best model:
Stepwise Selection
Stepwise selection methods automate the process of choosing variables but should be used with caution. They are particularly useful for large datasets or when exploring many potential predictors:
- Forward Selection: Begins with no variables and adds them one at a time based on significance.
- Backward Elimination: Starts with all variables and removes those that do not contribute meaningfully to the model.
These methods are useful when dealing with high-dimensional data, such as financial time series or macroeconomic indicators, where manually testing every variable is impractical.
Model Selection Using Economic Data
Let’s consider a practical example that ties together the insights from earlier posts. Suppose an economist is analyzing the relationship between GDP growth and macroeconomic variables such as interest rates, inflation, employment rates, and trade openness. The goal is to select the best regression model for predicting GDP growth:
- Initial Model: A multiple regression is run including all variables:\[ GDP \; growth = \beta_0 + \beta_1 \, Interest \; Rate + \beta_2 \, Inflation + \beta_3 \, Employment + \beta_4 \, Trade \; Openness + \epsilon \]
- Adjusted R2: Calculate the adjusted \( R^2 \) to assess how much variation in GDP growth is explained by the model. If the adjusted \( R^2 \) is low, it indicates that some variables may not be contributing significantly.
- AIC and BIC: Calculate AIC and BIC values for models with different subsets of variables. A model with fewer predictors that achieves a lower AIC or BIC is preferable.
- Mallows’ Cp: Evaluate the predictive power of different models using Mallows’ \( C_p \). A \( C_p \) value close to the number of predictors indicates a well-balanced model.
- Final Model: After evaluating these criteria, the final model might include only interest rates, inflation, and trade openness, providing a balance between accuracy and simplicity.
Challenges in Model Selection
Model selection is not always straightforward, and analysts may face several challenges:
- Limited Data: When data points are scarce, criteria like AIC and BIC may favor overly simple models.
- Outliers and Influential Points: Outliers can skew model selection criteria, leading to the choice of models that do not generalize well.
- Structural Breaks: In time series analysis, structural breaks can affect the stability of coefficients, making it necessary to test models over different time periods.
Addressing these challenges often involves using robust model diagnostics, testing for heteroscedasticity and autocorrelation, and relying on economic theory to guide variable selection.
Conclusion
Selecting the best econometric model is a crucial step that determines the reliability and interpretability of your results. Using criteria like adjusted R², AIC, BIC, and Mallows’ Cp allows you to identify a model that balances complexity and accuracy, providing meaningful insights into economic relationships. With a well-chosen model, econometric analysis becomes a powerful tool for making informed predictions, evaluating policies, and understanding economic dynamics.
This post builds on the knowledge from previous topics, providing a practical and comprehensive guide to model selection—an essential skill for any econometrician or data analyst working with economic data.
FAQs:
Why is model selection important in econometrics?
Model selection is crucial because it helps to find a balance between complexity and accuracy. The right model avoids overfitting (too complex) and underfitting (too simple), ensuring that relationships identified in the data are both statistically valid and economically meaningful.
What criteria are commonly used for selecting the best regression model?
Common criteria include Adjusted R², Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and Mallows’ Cp. These measures help in balancing the goodness of fit with model simplicity, aiding in the selection of the most appropriate model.
What is the difference between AIC and BIC?
AIC and BIC are both used to evaluate the fit of a regression model, but they differ in how they penalize complexity. AIC is less strict, making it suitable when the focus is on model fit, while BIC imposes a stronger penalty for adding more parameters, favoring simpler models.
How does stepwise regression help in model selection?
Stepwise regression automates variable selection by adding or removing predictors based on statistical significance. It includes methods like forward selection, which starts with no variables, and backward elimination, which starts with all variables. These techniques are useful for large datasets where manual testing is impractical.
What challenges can arise during model selection?
Challenges in model selection include limited data, outliers, and structural breaks in time series data. These issues can influence criteria like AIC and BIC, potentially leading to the selection of models that don’t generalize well. Addressing these challenges involves using robust diagnostics and incorporating economic theory to guide the selection process.
Thanks for reading! If you found this helpful, share it with friends and spread the knowledge.
Happy learning with MASEconomics



