Optimization techniques are critical in economics, helping individuals and organizations make the most efficient use of resources. Whether maximizing utility, minimizing costs, or finding an optimal solution to a complex problem, mathematical optimization tools like Newton’s Method and the Lagrange Multiplier Method are powerful allies in economic analysis.
Newton’s Method: Finding Optimal Points
What is Newton’s Method?
Newton’s Method is an iterative numerical technique used to find approximations of the roots (or zeros) of a real-valued function. In the context of economics, Newton’s Method can be applied to determine local extrema, such as maxima or minima, which can represent profit maximization, cost minimization, or utility optimization.
The general formula for Newton’s Method is:
\(x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}\)
In which:
- \(x_n\) is the current approximation.
- \(f(x_n)\) is the function evaluated at \(x_n\).
- \(f'(x_n)\) is the derivative of the function evaluated at \(x_n\).
This iterative approach helps refine the approximation until it converges to an optimal value or root.
Application in Economics: Cost Minimization
Consider a cost function \(C(x)\) that represents the cost of producing \(x\) units of a product. Newton’s Method can be used to determine the level of production that minimizes costs.
For example, suppose we have the following cost function:
\(C(x) = x^3 – 6x^2 + 11x – 6\)
To find the value of \(x\) that minimizes cost, we use Newton’s Method. First, we calculate the first derivative \(C'(x)\) and the second derivative \(C”(x)\):
\(C'(x) = 3x^2 – 12x + 11\)
\(C”(x) = 6x – 12\)
We then use the iterative formula to approximate the value of \(x\) that minimizes the cost. This is particularly useful for firms aiming to reduce production costs and achieve higher efficiency.
Lagrange Multiplier Method
Introduction to the Lagrange Multiplier Method
In economics, optimization problems often come with constraints. For instance, consumers maximize their utility subject to a budget constraint, or firms maximize their output given limited resources. The Lagrange Multiplier Method is a mathematical procedure used to find the local maxima and minima of a function subject to one or more constraints.
The general form of the Lagrange function is:
\(L(x_1, x_2, \ldots, x_n, \lambda) = f(x_1, x_2, \ldots, x_n) + \lambda \cdot \left( g(x_1, x_2, \ldots, x_n) – c \right)\)
In which:
- \(f(x_1, x_2, \ldots, x_n)\) is the objective function we wish to optimize.
- \(g(x_1, x_2, \ldots, x_n)\) is the constraint function.
- \(\lambda\) is the Lagrange multiplier, which represents the sensitivity of the objective function to the constraint.
Practical Example: Utility Maximization with Budget Constraint
Consider a consumer who wishes to maximize their utility from consuming two goods, \(x\) and \(y\), subject to a budget constraint. The utility function is given by:
\(U(x, y) = 2xy\)
The consumer has a budget of $60, with \(x\) (wine) costing $5 per unit and \(y\) (water) costing $1 per unit. The budget constraint can be expressed as:
\(5x + y = 60\)
We form the Lagrange function \(L(x, y, \lambda)\) as follows:
\(L(x, y, \lambda) = 2xy + \lambda(60 – 5x – y)\)
To find the optimal consumption bundle, we take the partial derivatives of \(L\) with respect to \(x\), \(y\), and \(\lambda\), and set them equal to zero:
Solving this system of equations, we find that the optimal consumption bundle is \(x = 6\) units of wine and \(y = 30\) units of water. The corresponding maximum utility is \(U(6, 30) = 360\) utility units.
Interpretation of the Lagrange Multiplier
The Lagrange multiplier \(\lambda\) has an important economic interpretation: it represents the marginal utility of income or the change in the objective function (e.g., utility or profit) for a one-unit increase in the constraint (e.g., income or budget). In our example, the value of \(\lambda = 12\) means that if the consumer’s budget were increased by $1, their utility would increase by 12 units.
Newton’s Method vs. Lagrange Method: When to Use Which?
Both Newton’s Method and the Lagrange Multiplier Method are valuable optimization tools, but they serve different purposes and are used in different contexts:
Newton’s Method is best suited for unconstrained optimization. It is highly efficient for finding local maxima or minima when there are no external limitations on the variables.
The Lagrange Multiplier Method is ideal for constrained optimization. It helps in finding optimal solutions when the decision-making process is restricted by certain conditions, such as budgets, resources, or other limitations.
Applications in Economic Analysis
Cost Minimization and Profit Maximization
Optimization techniques are widely used in cost minimization and profit maximization problems. Firms often face the challenge of minimizing their production costs subject to resource constraints or maximizing profits given the available technology and labor. By applying Newton’s Method, companies can find the optimal production level that minimizes costs. On the other hand, the Lagrange Multiplier Method can help determine how to allocate resources efficiently while respecting budgetary or capacity constraints.
Utility Optimization for Consumers
Consumers aim to achieve the highest level of satisfaction or utility given their budget constraints. By applying the Lagrange Multiplier Method, individuals can determine the optimal combination of goods and services that maximizes their utility while staying within their budget. This application is fundamental in understanding consumer choice theory and demand behavior.
Production Optimization
Another application of the Lagrange Multiplier Method is in production optimization. Suppose a firm is producing two goods and has limited access to raw materials and labor hours. The Lagrange Method allows the firm to find the optimal combination of inputs that maximizes output or minimizes costs, given the constraints on resources.
For instance, if a firm wants to maximize its output \(Q(x, y) = 4x^{0.5}y^{0.5}\) subject to labor and capital constraints, the Lagrange Method can be used to determine the optimal allocation of these resources to achieve maximum production.
Visualizing Optimization in Economics
Visual tools are immensely helpful in understanding the outcomes of optimization techniques in economics. In the case of Newton’s Method, a graphical representation of the function shows the points where the tangent intersects the x-axis, helping illustrate convergence to a root or extremum.
For the Lagrange Multiplier Method, graphical representations can depict indifference curves and budget constraints. The point at which an indifference curve is tangent to the budget line represents the optimal solution, which maximizes utility given the budget.
Below is a diagram illustrating the relationship between the indifference curve and the budget constraint. The point of tangency, marked as the optimal point, represents the combination of goods that maximizes consumer utility under the given budget.
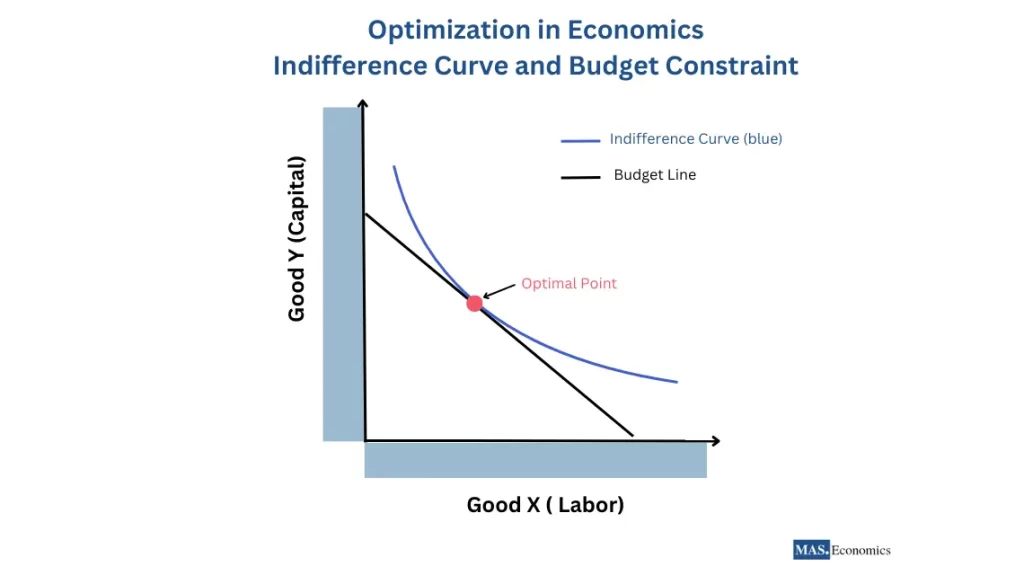
This visual aids in understanding how consumers allocate their resources efficiently to achieve the highest possible satisfaction within their budget limitations.
Conclusion
Optimization techniques like Newton’s Method and the Lagrange Multiplier Method are invaluable tools in economics, enabling economists and analysts to solve complex problems involving maximization and minimization. Newton’s Method is particularly useful for unconstrained problems, helping find optimal production levels or cost minimization points. The Lagrange Multiplier Method is indispensable when dealing with constraints, such as budgets or resource limitations, ensuring that solutions respect real-world limitations.
FAQs:
What is Newton’s Method, and how is it used in economics?
Newton’s Method is an iterative numerical technique used to approximate the roots of a function. In economics, it helps find optimal points, such as profit maxima or cost minima, by refining approximations of solutions. It works by evaluating the function and its derivative at a current point to predict the next approximation until convergence.
How is Newton’s Method applied to minimize costs?
To minimize costs using Newton’s Method, a firm analyzes its cost function by calculating the first and second derivatives. For example, if the cost function is \(C(q) = q^2 – 4q + 10\), Newton’s Method refines the solution iteratively until it identifies the production level that minimizes the cost.
What is the Lagrange Multiplier Method, and why is it important?
The Lagrange Multiplier Method is used for optimization problems with constraints. It helps find the maximum or minimum of a function subject to one or more constraints. The multiplier \(\lambda\) represents how much the objective function (e.g., utility or profit) changes with a one-unit change in the constraint (e.g., budget or resources).
How does the Lagrange Multiplier Method optimize utility?
In utility optimization, the Lagrange Method helps consumers find the optimal combination of goods to maximize satisfaction within their budget. If a consumer’s utility function is \(U(x, y) = x \cdot y\) and the budget constraint is \(5x + y = 60\), the method finds the quantities of goods \(x\) and \(y\) that maximize utility while respecting the budget.
What is the interpretation of the Lagrange multiplier?
The Lagrange multiplier \(\lambda\) measures the marginal impact of relaxing a constraint by one unit. In economic terms, it represents how much the objective function (e.g., utility or profit) increases with an additional dollar or resource unit added to the budget or production process.
When should Newton’s Method be used instead of the Lagrange Method?
Newton’s Method is suitable for unconstrained optimization problems, such as finding a profit-maximizing output where no budget or capacity restrictions exist. The Lagrange Method is ideal for constrained optimization, where factors like limited budgets, resources, or production capacity affect the solution.
How are these optimization methods applied in production and cost analysis?
Firms use Newton’s Method to find the production level that minimizes costs or maximizes profits. The Lagrange Method helps allocate resources efficiently when firms face constraints on inputs like labor or capital, maximizing output or minimizing costs while respecting these limitations.
Why is optimization important in economics?
Optimization ensures that individuals and firms use their resources efficiently to achieve maximum output, profit, or utility. By applying Newton’s and Lagrange’s methods, economists and decision-makers can make informed choices that maximize returns, minimize costs, and allocate resources effectively.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics