In economics, mathematical symbols are not just abstract notations—they are the language through which complex economic relationships are expressed. Understanding these symbols is essential if you want to navigate the equations and models that economists use to explain market behaviors, consumer choices, and policy impacts.
In this article, we will break down some of the most common mathematical symbols used in economics.
Why Understanding Mathematical Symbols Matters in Economics
Economic models, like those describing supply and demand, or the behavior of firms and consumers, rely heavily on mathematical notation. These symbols help economists simplify complex ideas into manageable parts, which makes the relationships clearer and easier to manipulate. Whether you’re an economics student or a professional in the field, learning how to read and interpret these symbols is critical to understanding the “language” of economics.
Mastery of these symbols helps you move beyond surface-level understanding to truly grasp how different economic factors interact, making it easier to conduct data-driven research, evaluate policies, and make strategic decisions.
The Symbols Economists Use Most Often
Economics borrows a lot from the world of mathematics, particularly algebra and calculus. Below, we’ll explore several key categories of symbols and their practical applications in economic contexts. Each of these symbols has a unique role in describing relationships and helping to quantify aspects of economic theory.
General Arithmetic Relations and Links
The foundation of economic equations lies in basic arithmetic operations. Understanding these fundamental symbols is crucial:
Equals Sign \((=)\)
The equals sign is probably the most straightforward of all symbols, representing equality between two sides of an equation. In economics, it is often used to describe a state of equilibrium—when supply equals demand, market forces are balanced, and prices are stable.
Example:
- \(Q_s = Q_d\) This equation denotes that the quantity supplied \((Q_s)\) is equal to the quantity demanded \((Q_d)\), indicating market equilibrium.
Not Equal To \((\neq)\)
This symbol represents inequality, a concept crucial in understanding market imbalances. For instance, if supply is not equal to demand, prices will adjust to reach a new equilibrium.
Example:
- \(P_1 \neq P_2\) Here, the price of one good is not equal to the price of another, which could be due to differences in quality or production costs.
Greater Than and Less Than \((>, <)\)
These symbols are used to compare quantities and are key in economic modeling, especially when analyzing constraints or optimization problems.
Example:
- \(Q_d > Q_s\) When demand \((Q_d)\) exceeds supply \((Q_s)\), the price is likely to increase.
Special Symbols and Their Role in Economics
Economics also employs a wide range of symbols beyond basic arithmetic to describe more sophisticated relationships.
Approximation \(a \approx b\)
Approximation is useful when perfect precision isn’t possible or necessary, particularly in macroeconomic models where rounding can make calculations more practical.
Example:
- If the annual GDP growth rate is 3.45%, we might say that \( \text{Growth} \approx 3.5\% \).
Definition
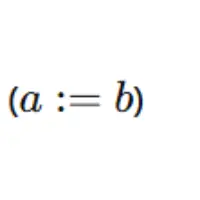
This symbol is used to define a term or variable clearly. For instance, if we want to establish what GDP per capita is, we could use:
Example:
Set Notation in Economics
Economists also use set notation to define possible values for certain economic variables. Understanding set notation helps us comprehend which values are feasible or allowed in a model.
Sets of Numbers
\((\mathbb{N}, \mathbb{Z}, \mathbb{R})\)
Economics frequently uses different sets of numbers:
- \(\mathbb{N}\): Natural numbers, used when we want to indicate that a value, such as the quantity of goods, cannot be negative.
- \(\mathbb{R}\): Real numbers, used for prices, which can take any value greater than or equal to zero.
Example:
- If \(x \in \mathbb{R}^+\), it means \(x\) is a positive real number—common when denoting prices or quantities.
Open and Closed Intervals
\(( [a, b], (a, b) )\)
Intervals are used to indicate a range of values, which can be open (excluding endpoints) or closed (including endpoints). These notations help define price ceilings or floors.
Example:
- \([0, 10]\): Indicates that the values can range from 0 to 10, including both 0 and 10, such as a price range set by regulation.
Understanding Limits in Economics
Limits are used in economics to explore the behavior of functions as they approach a specific value, often zero or infinity.
Limit Notation
\(\lim_{x \to a} f(x)\)
Limit notation helps economists understand marginal concepts—how small changes in a variable affect the outcome.
Example:
- Marginal Cost: The derivative of the cost function is found by taking the limit as the change in quantity approaches zero, which gives us the concept of marginal cost.
Infinity
\(\infty\)
Infinity is used when dealing with models that explore long-term outcomes. Understanding the behavior of an economic function as time approaches infinity is crucial for analyzing sustainable growth or debt stability.
Example:
- Debt Sustainability: \(\lim_{t \to \infty} D(t)\) analyzes if the debt level \(D(t)\) will stabilize over time or continue growing.
Practical Application of Mathematical Symbols in Economic Models
To truly grasp the value of these mathematical symbols, it’s useful to apply them in real-world economic contexts. Below are a few common applications:
Supply and Demand Models
Supply and demand equations often use basic arithmetic symbols (\(+, -, =\)) to represent equilibrium and shifts due to external factors like taxes or subsidies.
Example:
- \(Q_d = a – bP\): Demand as a function of price, where \(a\) and \(b\) are constants representing consumer preferences.
Utility Functions
In utility theory, mathematical symbols help economists describe the satisfaction a consumer gains from goods and services.
Example:
- \(U(x_1, x_2) = x_1^{\alpha}x_2^{1 – \alpha}\): A Cobb-Douglas utility function that uses exponents and arithmetic symbols to show the relationship between two goods.
Conclusion
Understanding mathematical symbols is foundational to learning economics. These symbols allow economists to express complex relationships succinctly, make precise calculations, and build models that explain the workings of markets, firms, and consumer choices. As you continue to encounter these symbols, remember that they are the keys to unlocking deeper insights into economic theory and real-world phenomena.
FAQs:
What are the most common arithmetic symbols used in economics?
Common arithmetic symbols include the equals sign (=) to indicate equilibrium, not equal to (≠) to show inequality, and greater than (>) or less than (<) for comparisons between quantities, crucial in supply-demand and optimization models.
How is the approximation symbol (≈) applied in economics?
The approximation symbol (≈) is used when precise values aren’t essential, such as rounding GDP growth rates or inflation figures, making economic models more practical without compromising insight.
What role does set notation play in economics?
Set notation defines feasible values for variables, such as quantities or prices, helping describe budget constraints, production possibilities, or ranges for regulated prices, like closed intervals [0,10].
How are real and natural numbers (ℝ and ℕ) relevant in economic models?
Natural numbers (ℕ) apply to discrete quantities like goods, while real numbers (ℝ) cover continuous variables such as prices or interest rates, reflecting the flexibility needed in different models.
Why are limits used in economic analysis?
Limits help examine marginal changes—such as marginal cost or marginal utility—by evaluating how a function behaves as variables approach a specific value, often zero or infinity.
How does the concept of infinity (∞) appear in economic models?
Infinity (∞) is used to analyze long-term behaviors, such as sustainable debt levels or economic growth, by examining whether variables stabilize or diverge over an extended period.
How are mathematical symbols applied in supply and demand models?
In supply and demand models, symbols express equilibrium (Qd = Qs) and shifts due to policy changes, like taxes, with equations representing how quantities respond to price changes.
Why is understanding mathematical notation important for economists?
Mathematical notation allows economists to express complex relationships precisely, facilitating clear communication, efficient modeling, and accurate policy evaluation in economic analysis.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics
